K-Means
K-Means clustering or simply clustering is an unsupervised learning technique. Unlike all the other techniques, which all came under supervised learning techniques, Kmeans is considered as unsupervised as there is no solid ground truth to compare our output with. It can only help us to determine the structure of our data and find smaller groups of data within our main data set.
The main goal is to divide our data into sub categories or clusters or we can say K pre-defined clusters. But how exactly do we create these clusters? Kmeans checks the similarities between different points and groups them in clusters. Remember the Euclidean distance that we discussed in KNN? We apply the same concept here as well in order to form our clusters. Let's understand the working using an example.
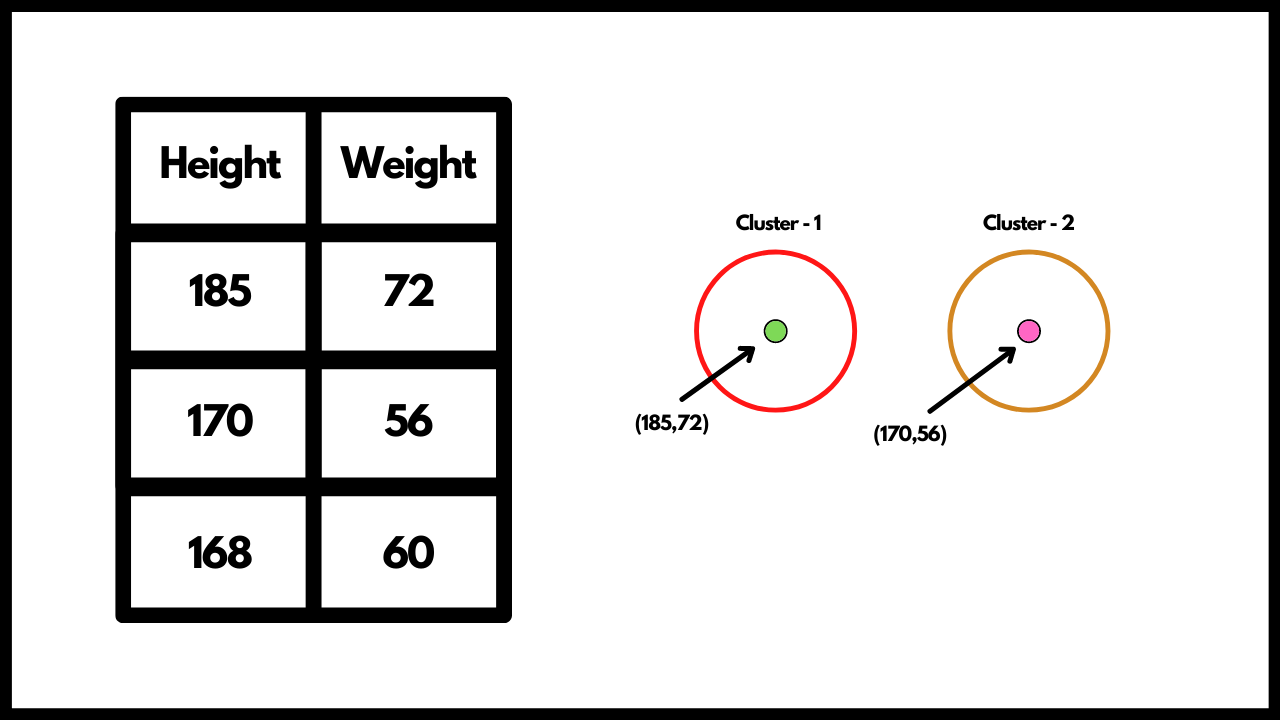
Let's say we are given a table with heights and weights of students and we need to perform clustering on it. In the above image we have 3 rows and 2 columns. We take the first point which forms our cluster one and we then take our second point which forms our second cluster. Now, when we bring in the third row entries, we need to check in which cluster does it belong, for that purpose we will be using our K1 which is our first point and K2 which is our second point and find the euclidean distance between them and the new point. The new point will become part of the cluster with which it has the least euclidean distance.

As we can see it has the least distance from K2 so it will become part of that cluster. Once we have found the cluster it belongs to , we need to recalculate the centroid for that cluster. This will give us a new centroid and whenever a new point enters, we will be using this new centroid to calculate the euclidean distance and this process goes on untill all the elements become part of some cluster. No point can be part of 2 clusters at the same time.
But again, how do we know what is the K value which is nothing but the optimal amount of Clusters required? For that we have something called the elbow method which helps us in selecting the optimal number of clusters. The idea is very simple. We need to calculate the sum of squared errors or SSE for each value of K in a given range. We will then plot a graph. It should look like an arm and the point where there is sudden dip in the plot or an 'elbow' is present, we take that K value to be the optimal K value. As we increase K value, the SSE tends to 0. So the goal is to choose a small value of K which also gives us a small SSE. We have already implemented this for you in the notebook below so you may go through them to understand it's implementation.
Let's quickly summarise what we just learnt:
- KMeans is a unsupervised learning technique.
- When we are trying to cluster our data points, we first set some random number of clusters or some random K value. And assign some centroids.
- Whenever we get a new point, we calculate the Euclidean distance between these points and the one that gives least euclidean distance, the new point will belong to that cluster.
- We then need to determine the new centroid of the cluster in which we add our target point.
- We repeat this for any new point that we have in our plane.
- To determine the optimal K value we can make use of elbow method to get better clusters.
With this we come to an end to the theory related to KMeans, you might go on to the Notebooks section followed by the Hand-On activity.
Implementation Walkthrough
Learn this section on Google Colab.